1. 选择方法
选择蓄能器时要涉及到许多参数,最重要的参数如下:
a. 最小压力P1和最大压力P2, 出于安全的原因,P2值必须低于或等于被选用的蓄能器所规定的最大工作压力。
b. 可储存或利用的液体容积△V, 为了正确确定蓄能器的尺寸,除了需要最大和最小压力以外还需要该数据。
c. 方法和用途
先确定运行中的气体是等温状态还是绝热状态:
例如压缩(或膨胀)进行得慢(大约3分钟),从而气体大约保持恒定的温度,该状态为等温。(例如:压力稳定、容积补偿、配重、润滑线路)。其它情况(蓄能、脉动缓冲、冲击缓冲等)由于传送速度高,热交换忽略不计,因此该状态为绝热当压缩或膨胀时间小于3分钟时,该绝热条件将作为先导而存在。
d. 工作温度
工作温度决定着胶囊材料和钢制壳体材料的选择,而且也对初始负载压力有影响,当然对蓄能器容积也有影响。
e. 液体种类决定材料的选择
f. 如所需大流量蓄能器,体积Vo和接头的规格与反应速度有关。
g. 使用场所
首先要了解蓄能器的最终使用场所在什么地方,以便使设计能够满足当地的设计参数和试验参数的要求。
根据上述内容,就能够为所要求的专门用途选择合适的蓄能器。
2. 预充气压力
正确选择预充气压力是获得蓄能器及其部件的最佳效率和最大使用寿命的基础。当预充气压力Po尽可能接近最小工作压力时,在理论上,能够获得液体的最大储量(或释放量)。
在实际应用中应给出安全系数。为了避免在运行中阀门关闭,此值(除非另有规定)为:
Po=0.9P1
Po的极限值为:Po min≥0.25×P2,Po max≤0.9P1
特殊值用于:
a. 脉动缓冲和减振
Po=0.6-0.75Pm 或 Po=0.8P1
式中: Pm= 平均工作压力.
b. 液路缓冲
Po=0.6-0.9Pm
式中: Pm=自由流动状态平均工作压力
c. 蓄能器+附加气瓶
Po=0.95-0.97P1 Po值适用于用户所要求的最大工作温度
通常对蓄能器的检验或预充压力是在与工作温度θ2不同的温度下进行的,因此Po值在检验温度θc时成为:
Poc=po![]()
若θc=20℃, 则Po(20℃)=Po![]()
注:蓄能器的预充压力直接由工厂在20℃的温度下完成,充注的气体是氮气。
3. 计算原理
蓄能器内部气体的压缩和膨胀是根据Boyle-Mariotte关于理想气体中状态变化的定律进行的:
Po×Von=P1×V1n= P2×V2n
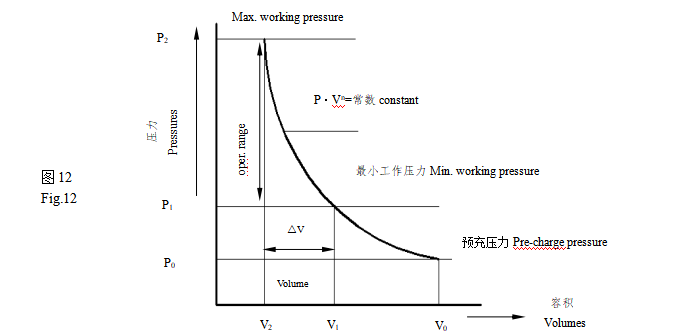
图12的PV图表示了蓄能器的“压力-容积”的关系。
Vo=压力Po时的预充氮气体积(升)
这是蓄能器能够储存的最大气体体积,它与额定容量相等或稍低一些。
V1=压力 P1时氮气体积(升)
V2=压力 P2时氮气体积(升)
V=排放或存储的液体容积(升)
Po=预充氮气压力(Bar)
P1=最小工作压力(Bar)
P2=最大工作压力(Bar)
n =多变指数
作为压力函数,容积变化曲线与n的幂有关,氮气的幂位于下述极限值之间:
n = 1 如果氮气的压缩和膨胀发生的很慢,使得整个热交换过程位于气体和周围介质之间,这就是在恒温下;该状态为等温。
这些都是理论状态而非实际状态。
然而能够合理精确的确定,当蓄能器用作容积补偿器、泄漏补偿或润滑补偿和压力补偿器,该状态为等温。在其他的用途中,例如用作能量储存器、脉动缓冲器、紧急动力源、动压力补偿器、减振器、液压弹簧等,应该确定该状态为绝热。
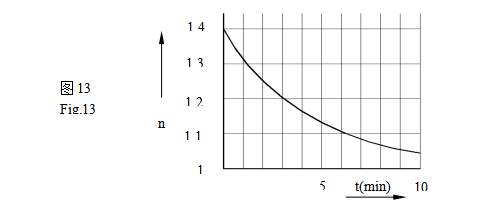
如果需要更精确的计算,可以使用n的中间值,n作为t的函数。如图13的曲线,n是膨胀时间或压缩时间的函数。
注:在计算中,压力用绝对巴表示,温度巴表示,温度用开氏度表示。
4. 容积计算(等温状态)
n = 1,Boyle-Mariott定律变为:
Po×Vo=P1×V1= P2×V2
因此 V1= Vo×![]() ;V2= Vo×
;V2= Vo× ![]()
容积V1(最小工作压力时)和V2(最大工作压力时)之间的差数给出所储存的液量。
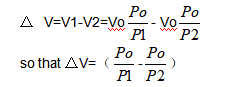
蓄能器容积将为 :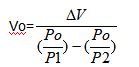
也可写作 : 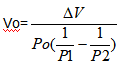
这说明当△V增加,Po下降,两个工作压力P1和P2之间的差数减小时,蓄能器的容积就增加。
5. 容积补偿(等温)
把蓄能器用作容积补偿的时候,是在等温状态下进行计算的一个典型的例子:
△V= Vt×(θ2-θ1)-(ß×3α)
式中:
Vt=管道容积 (升)
θ2 =最大温度(℃)
θ1= 最小温度(℃)
ß = 流体的体积膨胀系数(1/℃)
α = 管道线性膨胀系数(1/℃)
P1= 最小允许工作压力(bar)
P2= 最大允许工作压力(bar)
必须要的气体容积:
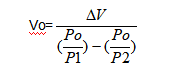
6. 泄漏补偿(等温)
蓄能器容积计算:
ΔV=Q1×t
Po=0.9×P1
P1=最小允许工作压力(bar)
P2=最大允许工作压力(bar)
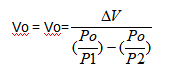
7. 容积计算(绝热状态)
从基本公式开始
Po×Von=P1×V1n= P2×V2n
如等温计算的情况一样,绝热状态容积计算时我们得到如下公式:
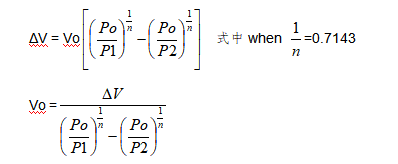
此公式在膨胀或压缩阶段的绝热状态时都有效。
B蓄能器的容积不仅会受到压力影响,还会受到工作温度的影响,在运行过程中工作温度会有很大的变化,在计算容积时要注意。温度和容积之间的关系是:
![]()
T2=2(℃)+273=最大工作温度(°K)
T1=1(℃)+273=最小工作温度(°K)
Vo=忽略了热变化而计算出的容积(升)
VoT=忽略了热变化而增加的容积(升)
8. 紧急能量存储
最典型的情况为储存进行的很慢(等温)而排放则很快(绝热)
气体容积由此式得出:
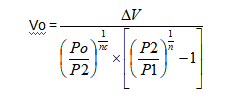
蓄能器容量由此式得出:
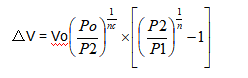
n =1.4 绝热系数(快速排放阶段)
nc = 1-1.4多变系数(慢速排放阶段)
此值是一个时间函数,可从图13的曲线推导出。
在大多数情况下,可以假设nc = 1,那么,计算就简化了,而且不影响结果
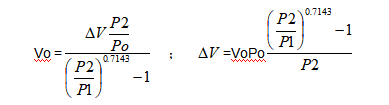
9.吸收脉动
典型的计算是在高速储存和排放的绝热状态下,计算时要考虑的液量△V与泵的型号及泵的工作容积有关
△V=k×q
容积则为:
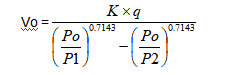
q=泵的工作容积(升)
=A×C(活塞面积×冲程)=Q/N(流率/冲程)
P=泵的平均工作压力(bar)
P1=P-X(bar) P2=P+X(bar)
α =剩余脉动±(%)
K=此为系数,它与活塞的数量及泵的单作用式及双作用式有关.
泵型号 K
1只活塞单作用式 0.69
1只活塞双作用式 0.29
2只活塞单作用式 0.29
2只活塞双作用式 0.17
3只活塞单作用式 0.12
3只活塞双作用式 0.07
4只活塞单作用式 0.13
4只活塞双作用式 0.07
5只活塞单作用式 0.07
5只活塞双作用式 0.023
6只活塞单作用式 0.07
7只活塞双作用式 0.023
10. 液压管线吸收冲击
流体的较高的加速或减速引起的压力迅速增加,通常称为水锤。超压的程度用ΔPmax来表示,它产生于管道关闭阀门的时候,受管道的长度、流速、流体的密度和阀门关闭的时间影响。
ΔPmax=2γLv/(t×105)
在预定的超压限制ΔP下,衰减冲击压力所需蓄能器的容积由下式给出:
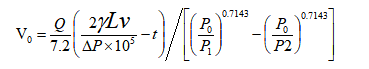
式中: V0=蓄能器容积 (升)
Q=管路中液体的流量 (m3/h)
L =管路总长(m)
V =流速 (m/s)= 103Q/3.6S
S =管路内截面积 (m m2)=πd2/4
d =管路内径(mm)
ΔP=允许超压值(bar)
P1 =管路的通常绝对压力值(absolute bar)
P2 =管路允许的最大绝对压力值 (absolute bar)= P1+ΔP
t=减速时间 (阀门关闭时间)(s)


